Quantifying the alignment of graph and features in deep learning

Abstract

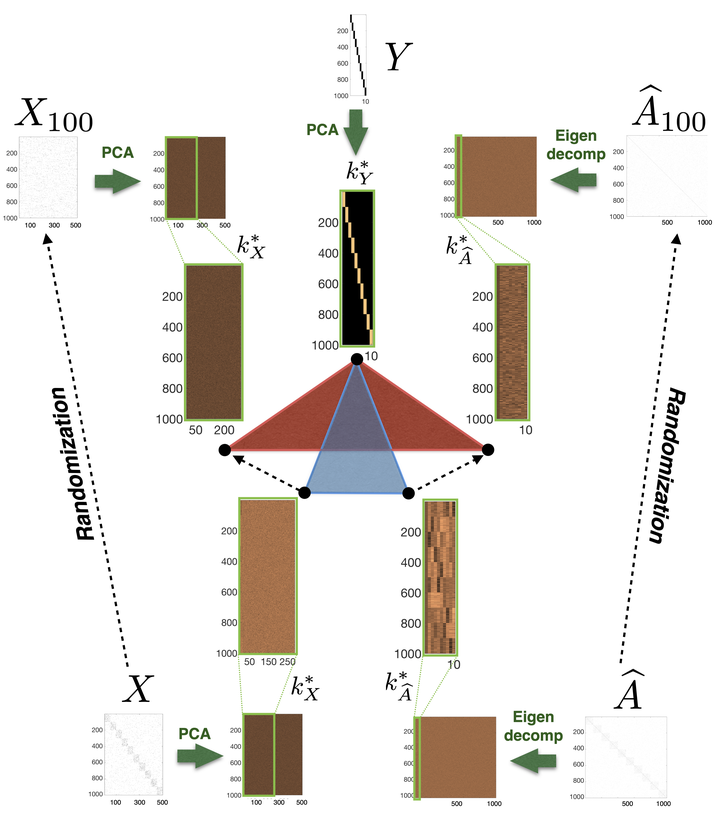
We show that the classification performance of Graph Convolutional Networks is related to the alignment between features, graph and ground truth, which we quantify using a subspace alignment measure corresponding to the Frobenius norm of the matrix of pairwise chordal distances between three subspaces associated with features, graph and ground truth. The proposed measure is based on the principal angles between subspaces and has both spectral and geometrical interpretations. We showcase the relationship between the subspace alignment measure and the classification performance through the study of limiting cases of Graph Convolutional Networks as well as systematic randomizations of both features and graph structure applied to a constructive example and several examples of citation networks of different origin. The analysis also reveals the relative importance of the graph and features for classification purposes.