Geometric graphs from data to aid classification tasks with graph convolutional networks

Abstract

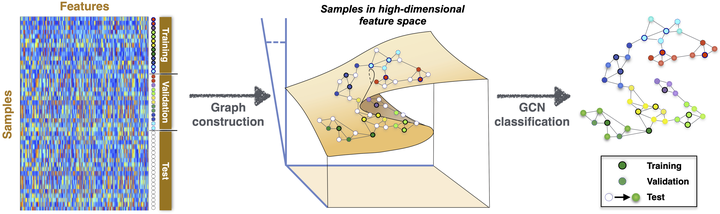
Traditional classification tasks learn to assign samples to given classes based solely on sample features. This paradigm is evolving to include other sources of information, such as known relations between samples. Here, we show that, even if additional relational information is not available in the dataset, one can improve classification by constructing geometric graphs from the features themselves, and using them within a Graph Convolutional Network. The improvement in classification accuracy is maximized by graphs that capture sample similarity with relatively low edge density. We show that such feature-derived graphs increase the alignment of the data to the ground truth while improving class separation. We also demonstrate that the graphs can be made more efficient using spectral sparsification, which reduces the number of edges while still improving classification performance. We illustrate our findings using synthetic and real-world datasets from various scientific domains.